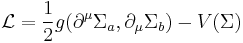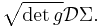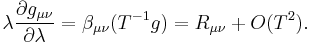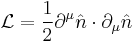Non-linear sigma model

In quantum field theory, a nonlinear σ model describes a scalar field Σ which takes on values in a nonlinear manifold called the target manifold T.

The target manifold is equipped with a Riemannian metric g. Σ is a differentiable map from Minkowski space M (or some other space) to T. The Lagrangian density is given by:

$\mathcal{L}={1\over 2}g(\partial^\mu\Sigma_a,\partial_\mu\Sigma_b)-V(\Sigma)$

where here, we have used a + - - - metric signature and the partial derivative 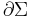$\partial\Sigma$ is given by a section of the jet bundle of T×M and V is the potential.

In the coordinate notation, with the coordinates Σ^a, a=1,...,n where n is the dimension of T,

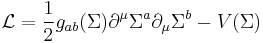$\mathcal{L}={1\over 2}g_{ab}(\Sigma) \partial^\mu \Sigma^{a} \partial_\mu \Sigma^{b} - V(\Sigma)$ .

In more than 2 dimensions, nonlinear σ models are nonrenormalizable. This means they can only arise as effective field theories. New physics is needed at around the distance scale where the two point connected correlation function is of the same order as the curvature of the target manifold. This is called the UV completion of the theory.

There is a special class of nonlinear σ models with the internal symmetry group G *. If G is a Lie group and H is a Lie subgroup, then the quotient space G/H is a manifold (subject to certain technical restrictions like H being a closed subset) and is also a homogeneous space of G or in other words, a nonlinear realization of G. In many cases, G/H can be equipped with a Riemannian metric which is G-invariant. This is always the case, for example, if G is compact. A nonlinear σ model with G/H as the target manifold with a G-invariant Riemannian metric and a zero potential is called a quotient space (or coset space) nonlinear σ model.

When computing path integrals, the functional measure needs to be "weighted" by the square root of the determinant of g

$\sqrt{\det g}\mathcal{D}\Sigma.$

This model proved to be relevant in string theory where the two-dimensional manifold is named worldsheet. Proof of renormalizability was given by Daniel Friedan.^[1] He showed that the theory admits a renormalization group equation, at the leading order of perturbation theory, in the form

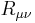$\lambda\frac{\partial g_{\mu\nu}}{\partial\lambda}=\beta_{\mu\nu}(T^{-1}g)=R_{\mu\nu}%2BO(T^2).$

being $R_{\mu\nu}$ the Ricci tensor. This represents a Ricci flow having Einstein equations for the target manifold as a fixed point. The existence of such a fixed point is relevant as it grants, at this order of perturbation theory, that conformal invariance is not lost due to quantum corrections and one has a sensible quantum field theory.

1 O(3) Non-linear Sigma Model
2 See also
3 Notes
4 External links

O(3) Non-linear Sigma Model

One of the most famous examples, of interest in for its particularly interesting topological properties, is the O(3) nonlinear sigma model in 1+1 dimension, with the Lagrange density

$\mathcal L= \frac{1}{2}\partial^\mu \hat n \cdot\partial_\mu \hat n$

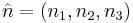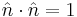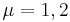where $\hat n=(n_1,n_2,n_3)$ with the constraint $\hat n\cdot \hat n=1$ and $\mu=1,2$ . This model allows for topological finite action solutions, as at infinite space-time the Lagrange density must vanish, meaning 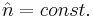$\hat n=const.$ at infinity. Therefore in the class of finite-action solutions we may identify the point at the infinity as a single point, i.e. that space-time can be identified with a Riemann Sphere. Since the 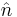$\hat n$ -field lives on a sphere as well, we have a mapping 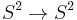$S^2\rightarrow S^2$ , the solutions of which are classified by the Second Homotopy group of a 2-sphere. These solutions are called the O(3) Instantons.

Notes

^ Friedan, D. (1980). "Nonlinear models in 2+ε dimensions". PRL 45 (13): 1057. Bibcode 1980PhRvL..45.1057F. doi:10.1103/PhysRevLett.45.1057. http://link.aps.org/doi/10.1103/PhysRevLett.45.1057.

External links

'Nonlinear Sigma model' on Scholarpedia

Quantum field theories

Standard	Chern–Simons model · Chiral model · Kondo model · Conformal field theory · Noncommutative quantum field theory · Non-linear sigma model · Quartic interaction · Quantum chromodynamics · Quantum electrodynamics · Quantum Yang–Mills theory · Schwinger model · Sine–Gordon · Standard Model · String theory · Toda field theory · Topological quantum field theory · Wess–Zumino model · Wess–Zumino–Witten model · Yang–Mills theory · Yang–Mills–Higgs model · Yukawa model · Thirring–Wess model

Four-fermion interactions	Thirring model · Gross–Neveu model · Nambu–Jona-Lasinio model

Non-linear sigma model

Contents

O(3) Non-linear Sigma Model

See also

Notes

External links